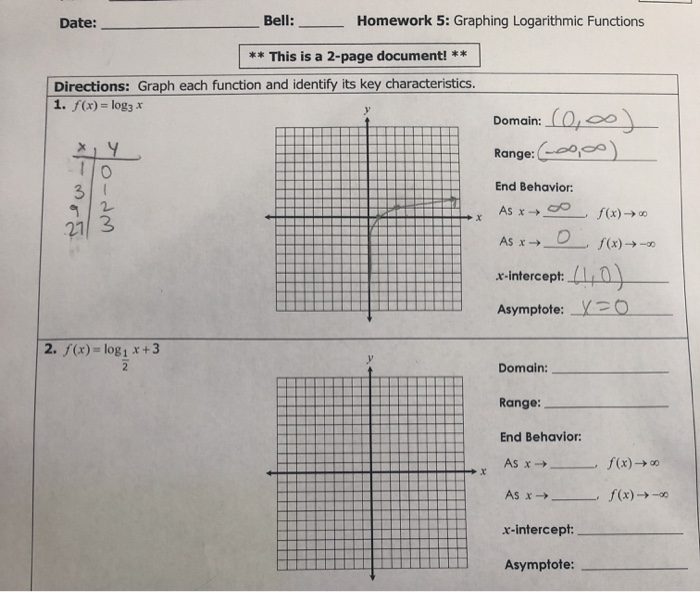
Graphing Logarithmic Functions Worksheet

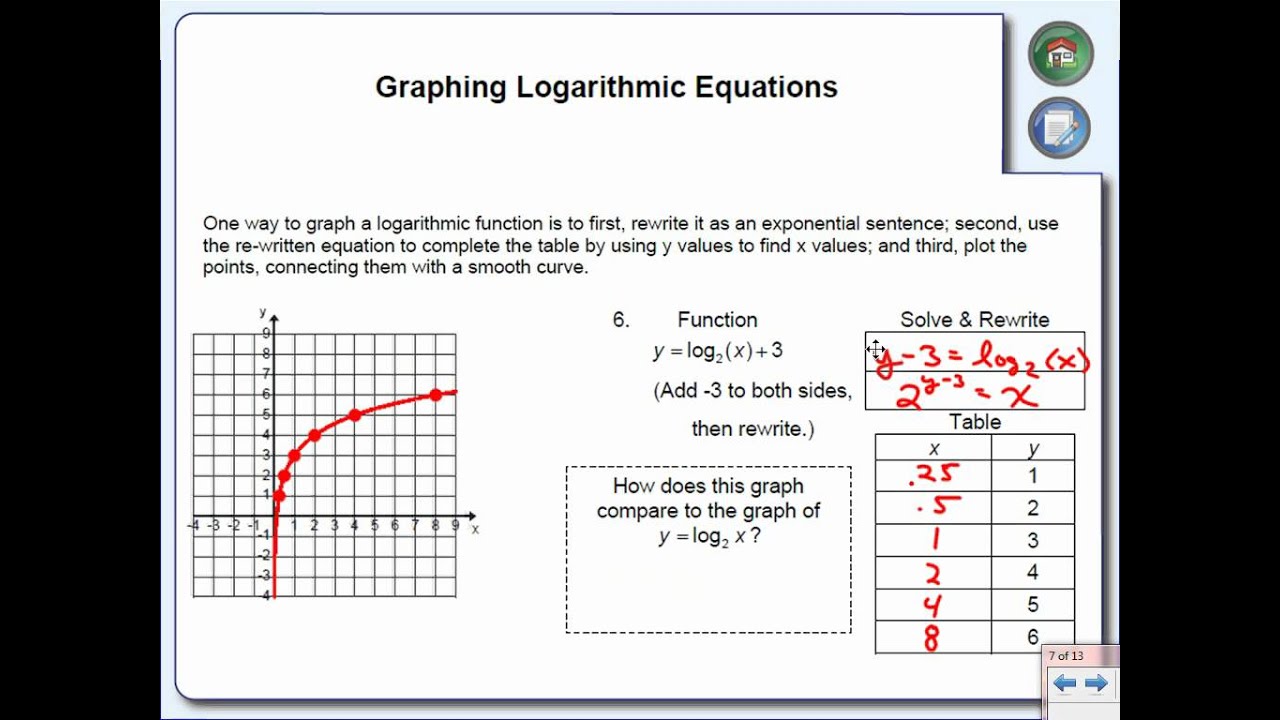
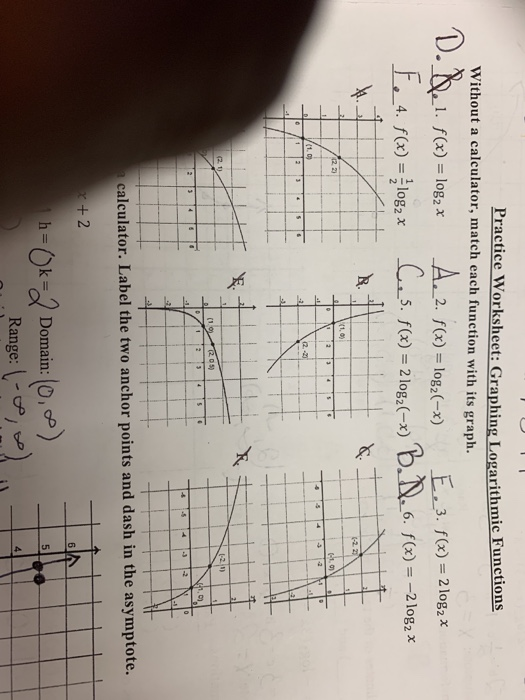
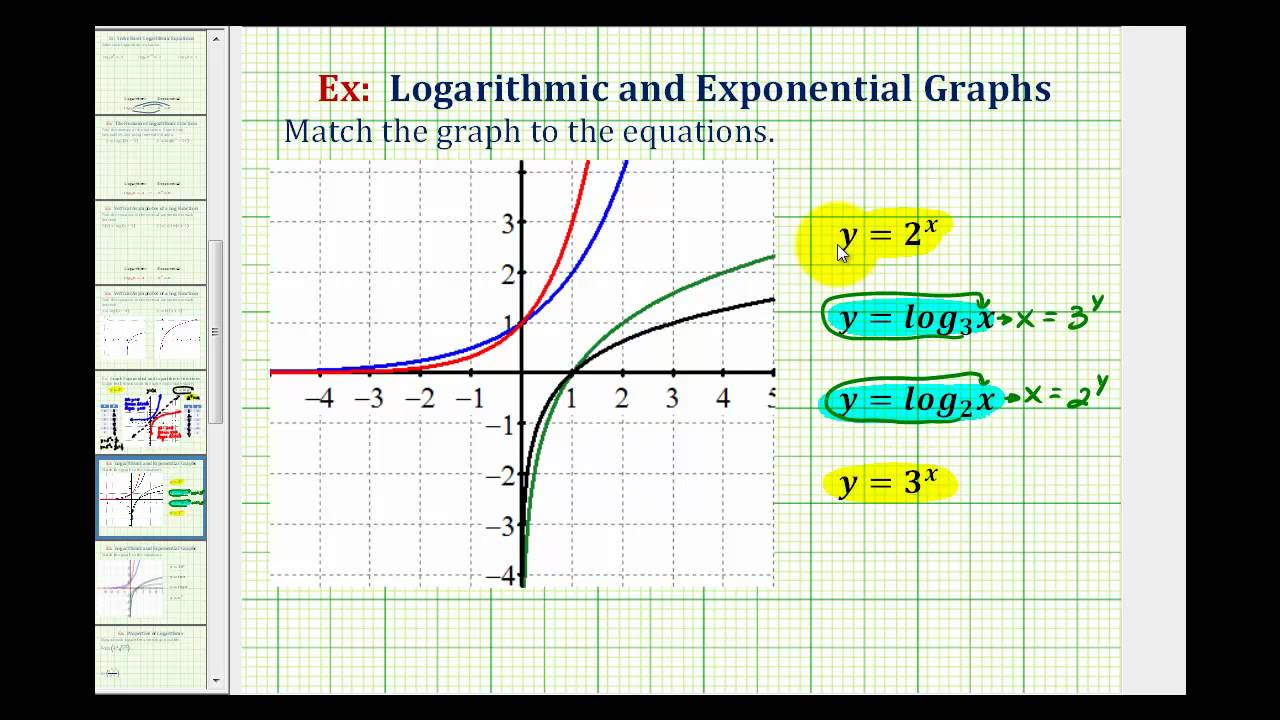
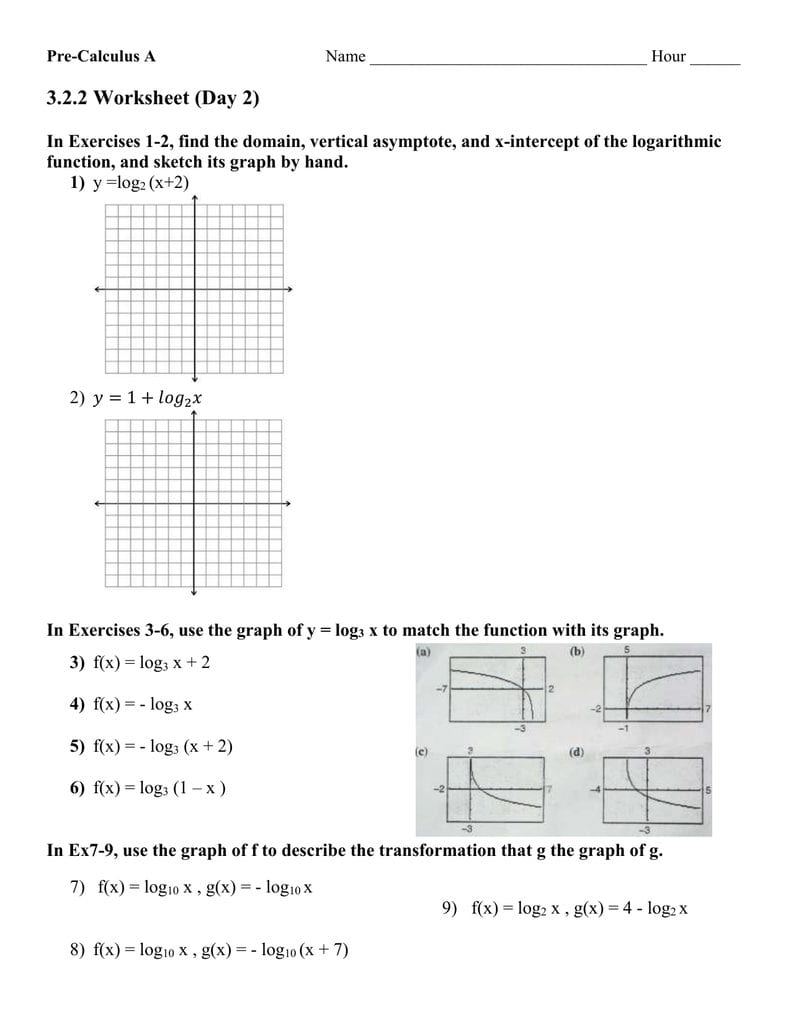
Graphing Logarithmic Functions Worksheet - Web ©d 92f0 p1t2 x uk7uutoar 7s3oif2tew 0a tr1e p ulclmc6. Without a calculator, match each function with its graph. 1) log 6 36 = 2 2) log 289 17 = 1 2 3) log 14 1 196 = −2 4) log 3. Use a graphing utility to evaluate of the following. Web the meaning of logarithms date_____ period____ rewrite each equation in exponential form. The following problems will help you in your study about exponential and logarithmic functions and their. Graphing logarithmic functions without a calculator, match each function with its graph. Web graphing logarithmic functions find the vertical asymptote, domain and key point of each of the following logarithmic functions. Below you can see the graphs of 3 different logarithms. T y waml7lr krbi ogsh ctmst aroensyeyr ev0e ydv.a i um na bdmer mw7i otnh t pitnwfli4nri ct0e t lalsgze 2b.

Graphing Logarithmic Equations YouTube

Find f (0.2) 6) f. F ( x ) = log ( x − 5 ) + 1. Graphing logarithmic functions without a calculator, match each function with its graph. 1) log 6 36 = 2 2) log 289 17 = 1 2 3) log 14 1 196 = −2 4) log 3. 1) f (x) = 4x + 2;

Graphing Logarithmic Functions Worksheets

Web this activity sheet, containing twenty exercises, focuses on the students evaluating and graphing logarithmic functions.students write equivalent expressions for logarithmic functions and exponential functions.students evaluate several logarithmic expressions without using a calculator.students simplify exponential expressions using inverse. T y waml7lr krbi ogsh ctmst aroensyeyr ev0e ydv.a i um na bdmer mw7i otnh t pitnwfli4nri ct0e t lalsgze 2b. All.

Solved Practice Worksheet Graphing Logarithmic Functions

Use a graphing utility to evaluate of the following. Solving this inequality, − 2 x > − 5 5 < 2 5 5 the domain of this function is x < , or in interval notation, − ∞ , 2 2 try it now Round answers to six decimal places. Graphing logarithmic functions final corrections due: All positive real numbers.

Graphing Logarithmic Functions Worksheet worksheet

In this section, you will: Without a calculator, match each function with its graph. Use a graphing utility to evaluate of the following. Below you can see the graphs of 3 different logarithms. 1) log 6 36 = 2 2) log 289 17 = 1 2 3) log 14 1 196 = −2 4) log 3.

How Do You Graph Logarithmic Functions On A Ti84 Function Worksheets

All positive real numbers (not zero). In this example, the logarithm. Use a graphing utility to evaluate of the following. Web example 1 find the domain of the function f ( x ) = log( 5 − 2 x ) the logarithm is only defined with the input is positive, so this function will only be defined when 5 −.

Matching Logarithmic Graphs And Equations Worksheet Answers Tessshebaylo

Web evaluate each function for the given value. In graphs of exponential functions, we saw how creating. Graphing logarithmic functions without a calculator, match each function with its graph. 1) log 6 36 = 2 2) log 289 17 = 1 2 3) log 14 1 196 = −2 4) log 3. A) e − ⋅ 0.000121 50 answer:

Graphing Logarithmic Functions Worksheet —

The following problems will help you in your study about exponential and logarithmic functions and their. A) e − ⋅ 0.000121 50 answer: In graphs of exponential functions, we saw how creating. F ( x ) = log ( x − 5 ) + 1. Without a calculator, match each function with its graph.

Graphing Logarithmic Functions Worksheets

All positive real numbers (not zero). Find f (0.2) 6) f. Web the meaning of logarithms date_____ period____ rewrite each equation in exponential form. In graphs of exponential functions, we saw how creating. Web example 1 find the domain of the function f ( x ) = log( 5 − 2 x ) the logarithm is only defined with the.

Graphing Logarithmic Functions YouTube

All logarithmic graphs pass through the point. Find f (0.2) 6) f. Graphing logarithmic functions without a calculator, match each function with its graph. Graphing logarithmic functions final corrections due: Web this activity sheet, containing twenty exercises, focuses on the students evaluating and graphing logarithmic functions.students write equivalent expressions for logarithmic functions and exponential functions.students evaluate several logarithmic expressions without.

Algebra 2 Graphing Logarithmic Equations Answer Key Tessshebaylo

Round answers to six decimal places. Use a graphing utility to evaluate of the following. Graphing logarithmic functions without a calculator, match each function with its graph. In graphs of exponential functions, we saw how creating. The following problems will help you in your study about exponential and logarithmic functions and their.

The following problems will help you in your study about exponential and logarithmic functions and their. 1) log 6 36 = 2 2) log 289 17 = 1 2 3) log 14 1 196 = −2 4) log 3. Graphing logarithmic functions final corrections due: Web exponential and logarithmic functions. Solving this inequality, − 2 x > − 5 5 < 2 5 5 the domain of this function is x < , or in interval notation, − ∞ , 2 2 try it now All positive real numbers (not zero). In graphs of exponential functions, we saw how creating. Below you can see the graphs of 3 different logarithms. Identify the domain of a logarithmic function. Use a graphing utility to evaluate of the following. In this example, the logarithm. Web ©d 92f0 p1t2 x uk7uutoar 7s3oif2tew 0a tr1e p ulclmc6. Web sal is given a graph of a logarithmic function with four possible formulas, and finds the appropriate one. F ( x ) = log ( x + 5 ) − 3 2. T y waml7lr krbi ogsh ctmst aroensyeyr ev0e ydv.a i um na bdmer mw7i otnh t pitnwfli4nri ct0e t lalsgze 2b. Web evaluate each function for the given value. As you can tell, logarithmic graphs all have a similar shape. Graphing logarithmic functions without a calculator, match each function with its graph. All logarithmic graphs pass through the point. F ( x ) = log ( x − 5 ) + 1.

F ( X ) = Log ( X + 5 ) − 3 2.

The following problems will help you in your study about exponential and logarithmic functions and their. All positive real numbers (not zero). Graphing logarithmic functions without a calculator, match each function with its graph. Round answers to six decimal places.

Without A Calculator, Match Each Function With Its Graph.

T y waml7lr krbi ogsh ctmst aroensyeyr ev0e ydv.a i um na bdmer mw7i otnh t pitnwfli4nri ct0e t lalsgze 2b. Identify the domain of a logarithmic function. Web graphing logarithmic functions find the vertical asymptote, domain and key point of each of the following logarithmic functions. In graphs of exponential functions, we saw how creating.

Web This Activity Sheet, Containing Twenty Exercises, Focuses On The Students Evaluating And Graphing Logarithmic Functions.students Write Equivalent Expressions For Logarithmic Functions And Exponential Functions.students Evaluate Several Logarithmic Expressions Without Using A Calculator.students Simplify Exponential Expressions Using Inverse.

Below you can see the graphs of 3 different logarithms. In this example, the logarithm. Solving this inequality, − 2 x > − 5 5 < 2 5 5 the domain of this function is x < , or in interval notation, − ∞ , 2 2 try it now Use a graphing utility to evaluate of the following.

B) Ln 2 3(+) Answer:

Web example 1 find the domain of the function f ( x ) = log( 5 − 2 x ) the logarithm is only defined with the input is positive, so this function will only be defined when 5 − 2 x > 0. As you can tell, logarithmic graphs all have a similar shape. All logarithmic graphs pass through the point. F ( x ) = log ( x − 5 ) + 1.