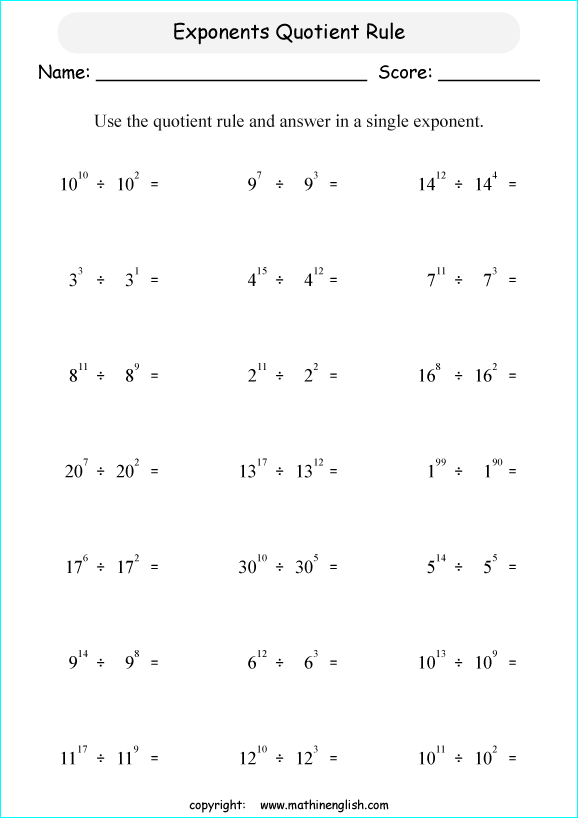Properties Of Exponents Worksheet

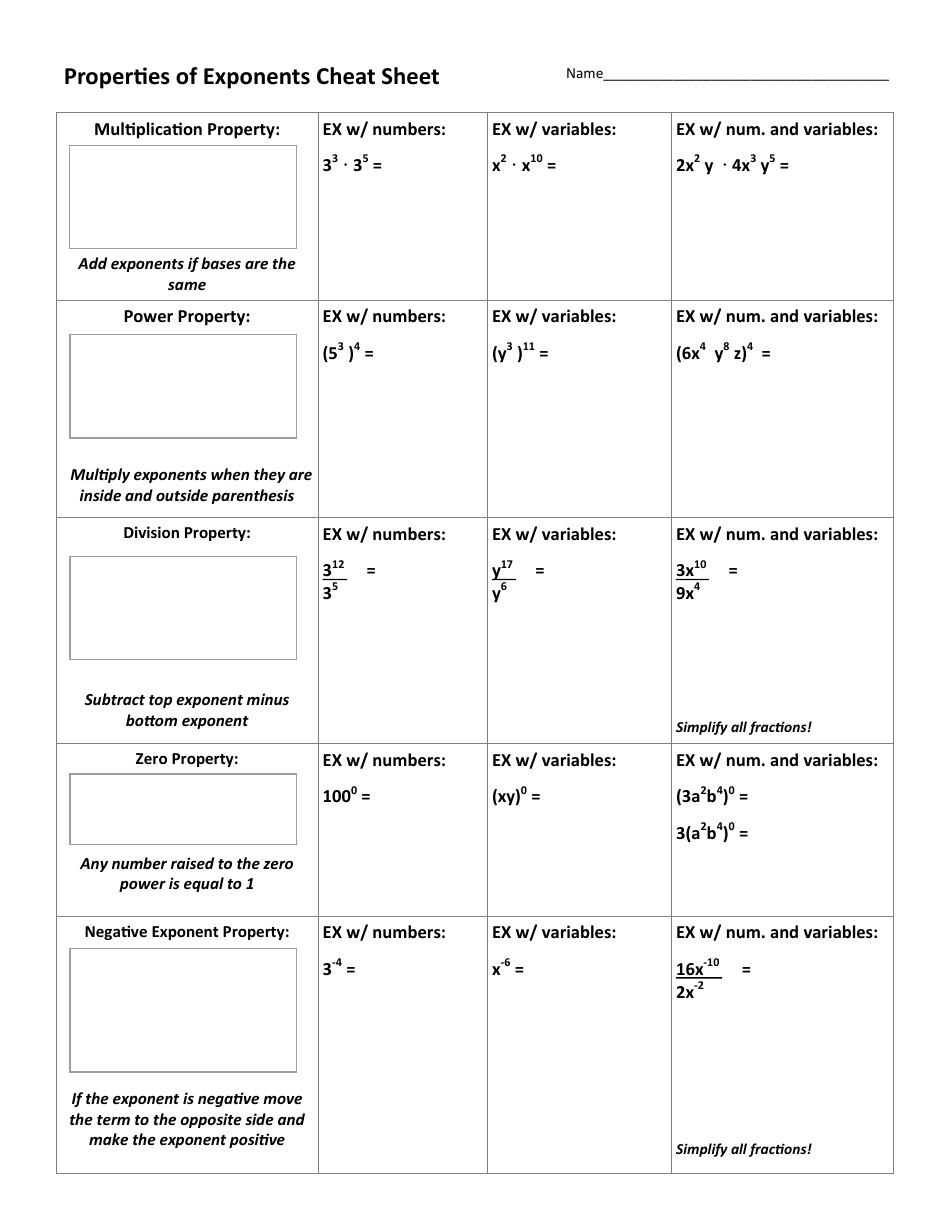
Properties Of Exponents Worksheet - Answers should have positive exponents only and all numbers evaluated, for example 53 = 125. Web let’s begin by stating the properties of exponents. Your answer should contain only positive exponents. Our exponents worksheets are free to download, easy to use, and very flexible. It is important to note that none of these applications can occur if the bases are not the same. Web properties of exponents simplify. Power of a quotient property. Power of a product property ac ⋅ bc = (ab)c, a, b ≠ 0 a c ⋅ b c = ( a b) c, a, b ≠ 0. Your answer should contain only positive exponents. 1) 2 m2 ⋅ 2m3 2) m4 ⋅ 2m−3 3) 4r−3 ⋅ 2r2 4) 4n4 ⋅ 2n−3 5) 2k4 ⋅ 4k 6) 2x3 y−3 ⋅ 2x−1 y3 7) 2y2 ⋅ 3x 8) 4v3 ⋅ vu2 9) 4a3b2 ⋅ 3a−4b−3 10) x2 y−4 ⋅ x3 y2 11) (x2) 0 12) (2x2) −4 13) (4r0) 4 14) (4a3) 2

Free exponents worksheets

Using a combination of rules at one point, you may be asked to use a combination of these properties. Web in this lesson, you will learn some properties that will help you simplify exponential expressions containing multiplication. Web below is a list of properties of exponents: Your answer should contain only positive exponents. The expression n a is called a.

Exponents (8.EE.1 8.EE.2) Strickler WMS

Our exponents worksheets are free to download, easy to use, and very flexible. Product of powers property ab ⋅ ac = ab+c, a ≠ 0 a b ⋅ a c = a b + c, a ≠ 0. Using a combination of rules at one point, you may be asked to use a combination of these properties. $ % $.

Free Printable Exponent Worksheets Printable Worksheets

Our exponents worksheets are free to download, easy to use, and very flexible. It is important to note that none of these applications can occur if the bases are not the same. Your answer should contain only positive exponents. Power of a quotient property. Order of operations with exponents.

Properties of Exponents Worksheet With Answer Key Download Printable

Order of operations with exponents. Our exponents worksheets are free to download, easy to use, and very flexible. Web more properties of exponents date_____ period____ simplify. Using a combination of rules at one point, you may be asked to use a combination of these properties. An the number a is the __________, and the number n is the ______________________.

Properties Of Exponents Worksheet —

The expression n a is called a power and is read “ a to the n th power.” let’s try some examples. Product of powers property ab ⋅ ac = ab+c, a ≠ 0 a b ⋅ a c = a b + c, a ≠ 0. 1) 2 m2 ⋅ 2m3 2) m4 ⋅ 2m−3 3) 4r−3 ⋅ 2r2.

Properties of Exponents Worksheet With Answer Key Download Printable

Review the common properties of exponents that. The expression n a is called a power and is read “ a to the n th power.” let’s try some examples. Our exponents worksheets are free to download, easy to use, and very flexible. 1) 2 m2 ⋅ 2m3 2) m4 ⋅ 2m−3 3) 4r−3 ⋅ 2r2 4) 4n4 ⋅ 2n−3 5).

Practice Worksheet Properties Of Exponents

$ % $ % &'()* +( , Your answer should contain only positive exponents. Your answer should contain only positive exponents. Order of operations with exponents. Web properties of exponents date_____ period____ simplify.

Properties Of Exponents Worksheet Answers —

Web in this lesson, you will learn some properties that will help you simplify exponential expressions containing multiplication. Properties of exponents simplify each expression completely using properties of exponents. Your answer should contain only positive exponents. Web properties of exponents date_____ period____ simplify. Product of powers property ab ⋅ ac = ab+c, a ≠ 0 a b ⋅ a c.

Properties of Exponents worksheet

Web let’s begin by stating the properties of exponents. Using a combination of rules at one point, you may be asked to use a combination of these properties. For example, cannot be simplified. Your answer should contain only positive exponents. Review the common properties of exponents that.

Multiplication Properties Of Exponents Worksheet

Web properties of exponents date_____ period____ simplify. Our exponents worksheets are free to download, easy to use, and very flexible. Using a combination of rules at one point, you may be asked to use a combination of these properties. The expression n a is called a power and is read “ a to the n th power.” let’s try some.

Answers should have positive exponents only and all numbers evaluated, for example 53 = 125. Web let’s begin by stating the properties of exponents. Power of a product property ac ⋅ bc = (ab)c, a, b ≠ 0 a c ⋅ b c = ( a b) c, a, b ≠ 0. Your answer should contain only positive exponents. The expression n a is called a power and is read “ a to the n th power.” let’s try some examples. Review the common properties of exponents that. Properties of exponents simplify each expression completely using properties of exponents. It is important to note that none of these applications can occur if the bases are not the same. Our exponents worksheets are free to download, easy to use, and very flexible. Web we have evaluating exponents functions, graphing exponents, properties of exponents, writing numbers in scientific notation, and operations with scientific notation. An the number a is the __________, and the number n is the ______________________. Power of a quotient property. 1) 2 m2 ⋅ 2m3 2) m4 ⋅ 2m−3 3) 4r−3 ⋅ 2r2 4) 4n4 ⋅ 2n−3 5) 2k4 ⋅ 4k 6) 2x3 y−3 ⋅ 2x−1 y3 7) 2y2 ⋅ 3x 8) 4v3 ⋅ vu2 9) 4a3b2 ⋅ 3a−4b−3 10) x2 y−4 ⋅ x3 y2 11) (x2) 0 12) (2x2) −4 13) (4r0) 4 14) (4a3) 2 $ % $ % &'()* +( , Web properties of exponents simplify. For example, cannot be simplified. Web below is a list of properties of exponents: Your answer should contain only positive exponents. Web in this lesson, you will learn some properties that will help you simplify exponential expressions containing multiplication. Using a combination of rules at one point, you may be asked to use a combination of these properties.

Web More Properties Of Exponents Date_ Period Simplify.

Power of a quotient property. Our exponents worksheets are free to download, easy to use, and very flexible. Product of powers property ab ⋅ ac = ab+c, a ≠ 0 a b ⋅ a c = a b + c, a ≠ 0. Web below is a list of properties of exponents:

Power Of A Product Property Ac ⋅ Bc = (Ab)C, A, B ≠ 0 A C ⋅ B C = ( A B) C, A, B ≠ 0.

The expression n a is called a power and is read “ a to the n th power.” let’s try some examples. Review the common properties of exponents that. Web properties of exponents date_____ period____ simplify. Order of operations with exponents.

1) 2 M2 ⋅ 2M3 2) M4 ⋅ 2M−3 3) 4R−3 ⋅ 2R2 4) 4N4 ⋅ 2N−3 5) 2K4 ⋅ 4K 6) 2X3 Y−3 ⋅ 2X−1 Y3 7) 2Y2 ⋅ 3X 8) 4V3 ⋅ Vu2 9) 4A3B2 ⋅ 3A−4B−3 10) X2 Y−4 ⋅ X3 Y2 11) (X2) 0 12) (2X2) −4 13) (4R0) 4 14) (4A3) 2

Your answer should contain only positive exponents. Web properties of exponents simplify. Answers should have positive exponents only and all numbers evaluated, for example 53 = 125. Web in this lesson, you will learn some properties that will help you simplify exponential expressions containing multiplication.

Web Let’s Begin By Stating The Properties Of Exponents.

Using a combination of rules at one point, you may be asked to use a combination of these properties. $ % $ % &'()* +( , Properties of exponents simplify each expression completely using properties of exponents. For example, cannot be simplified.